How to Find Scale Factor in Two- and Three-Dimensional Geometry
In two and three-dimensional geometry, a scale factor is a ratio between two linear measurements. You can use scale factors to determine the surface area of an object. The first step in using scale factors is to understand why you might need one. Here’s a look at a few examples. A scale factor can be useful in a variety of situations. For example, if you want to calculate a certain percentage increase for an item, you can multiply the total amount by a certain scale factor.
Objects can be enlarged or reduced by a scale factor
An object’s size can be enlarged or reduced by a factor called a scale factor. This is the number multiplied by the entire object’s components to get the desired scale. It is similar to a unit scale, but without units. Scale factors are proportional to the scaled measurement.
The basic formula for finding the scale factor is: Dimension of new shape / Dimension of original shape. This scale factor enables a person to see a large object in a small space. It is also used to create scale plans and blueprints for architecture and machinery. It also makes it possible to shrink vast lands.
The term “scale factor” is used to refer to the ratio of one object’s dimensions to another object. For example, if an object has side lengths of three centimeters, then a scaling factor of four would produce a triangle with four centimeters in length. In the same manner, a rectangle can be reduced to one centimeter in size by multiplying the original dimensions by a scale factor of three.
When drawing objects, you can use a scale factor to create an accurate representation. Scale factors are used to make figures of any size look larger or smaller than they would otherwise be. This is a useful technique for architects and designers to manipulate models that would otherwise be impossible to handle at full size.
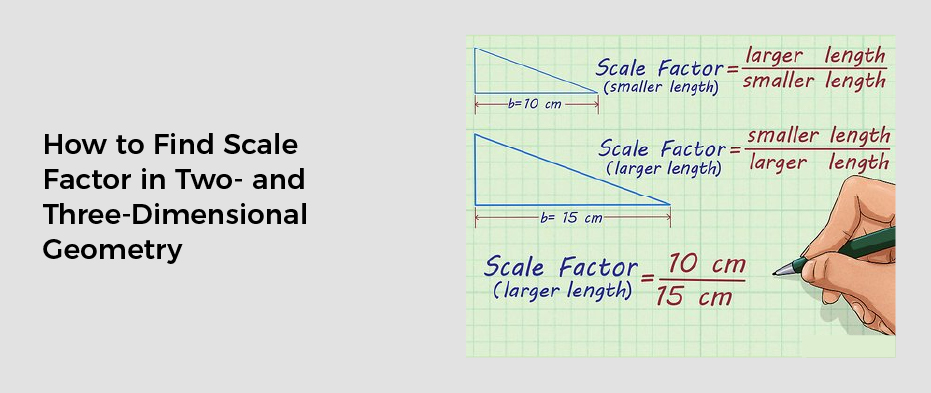
It is a ratio of linear measurements
The scale factor is a ratio that describes how different geometric figures compare to each other. It can be expressed in any unit, and can be useful for solving geometric problems. For example, if two shapes have similar side lengths, then their scale factor will be the same. If they have different lengths, the scale factor will be different.
If a figure is 16 feet long and the map shows it as 4 inches, then the scale factor is 148. This means that the real distance is actually twelve times larger than the map. It also allows for a conversion between the two measurements, so you can see that an 8-foot fence on a drawing equals a 16-foot fence in real life.
The simplest way to express a scale factor is as a ratio. For example, if two identical rhombuses have sides of 48 square meters and one is one hundred and eighty square meters, the scale factor would be 148. The area of each is the same, but the scale factor would affect the sides, angles, and perimeter.
A scale factor is used to multiply the size of a model or drawing to its real size. It allows you to make a shed that is 32 feet long into 4.4 inches long. Then, you can multiply that by the size of the model parts. With this equation, you will have an accurate representation of the original size.
It is used in two-dimensional and three-dimensional geometry
In two-dimensional and three-dimensional geometry, a scale factor is a measure of how much one shape or figure can be enlarged or reduced. In other words, it is the ratio of one figure’s side to the corresponding side of another figure. Using the scale factor in a drawing will help you draw larger or smaller versions of a figure.
To understand scale factor in two-dimensional and three-dimensional geometry, consider the following example: You have an original rectangle that has three sides and two corners. If you multiply this number by three, you will get a second figure that is one-seventh the original size.
It can be used to calculate surface area
The scale factor is a measure of the ratio between two linear measurements. For example, if a distance is 1 in on the map and 12 feet in the real world, the real distance is 12 times bigger. The scale factor in one direction is a/b, while the scale in the other direction is c/d. Hence, a First Area (ac) is actually bd in size. The scale factor is equal to the ratio bd/ac.
Students can explore different scale factors by investigating different shapes. A good example is the equilateral triangle. They can investigate the effect of different scale factors on the area of an equilateral triangle, or on the volume of a non-equilateral triangle. They can also experiment with irregular shapes, and the simple special case of a rectangle.
Another example is to compare two similar solids with different volumes. A rectangular prism has the same volume as a cube with the same surface area, but a cube has a larger volume. This means that the larger solid has more surface area than the smaller one.
For example, a sardine factory uses steel cans that are cylinder-shaped. An engineer would like to calculate the area of the label on a can. He would enter these two measurements into a formula to calculate the lateral surface area. In addition, a cylindrical water tank will be painted blue. The total surface area should be rounded to the nearest hundredth.
It can be used to calculate volume
A scale factor can be used to calculate volume. A solid can have different volumes based on the scale factor. For example, a prism with a volume of 5 cubic feet can have a different volume compared to one that is 10 cubic feet. You can use a graph to show this relationship. To create a graph, you can create a table with the values of each parameter and connect them with a smooth curve.
The same method can be applied to other solids. The simplest case is to work with a unit cube. Alternatively, you can use a pile of small cubes to create larger ones. You can then count the area and volume of each of the new shapes. You can even find the scale factor for both area and volume to investigate the relationship.